は1 つの直線 yax b のまわりに集まって いると考えられる。簡単に言えば,この直線が回帰直線である。ただし,回帰直線は,相関とは無 関係に定義できる。回帰直線の考え方は,以下の通りである。 (1) x の値から y の値を予測するための最適な直線を点と直線の距離を求める公式 まず「点と直線の距離」ときいて、何を思い浮かべますか? 図のような点Pと直線lの距離を求める方法についてみていきましょう。 図のように、直線l:"ax+by+c=0"上にY=mxn の直線の方程式 最初に、中学数学で扱った y=mxn 型の直線の方程式について復習します。 y=mxn の直線の方程式は、 m が直線の傾き、 n が y 切片を表しています。 傾きとは、 x 軸方向に 1 進んだときにどれだけ y 座標が上がるかを表しています。 axbyc=0 の直線の方程式
点と直線の距離
直線 の 公式
直線 の 公式-2 回帰直線 相関係数 変量間の直線的関連性の強さを測る尺度 2つの変量間の関係を直線で表現する方法を考える 測定の難しい変量を,測定が容易な変量を用いて推測する ある変量を,他の変量から予測する 基本的な考え方 2つの変量に直線的な関係を仮定し,Mar 06, 21 · 二点を通る直線の方程式1 冒頭の表現は教科書にも載っている最も基本的な形式です。 基本的にはこの公式1で覚えておけ
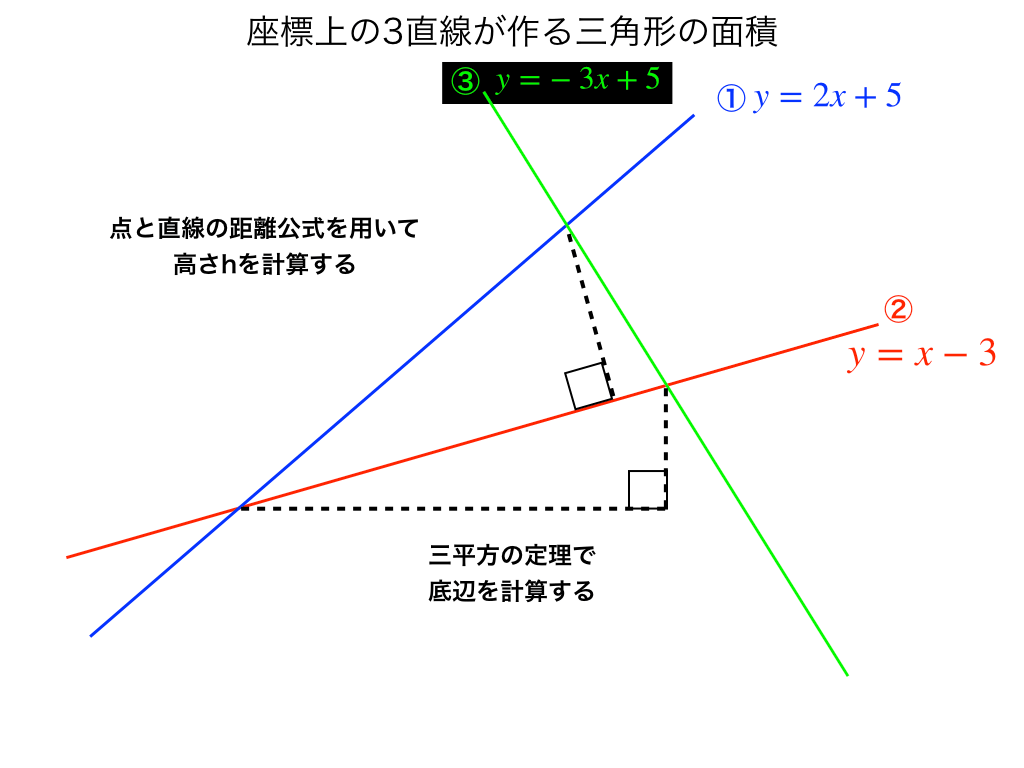


三角形の成立条件と面積の求め方を解説 図形と方程式
直線の方程式は であるので、外積は、 これらのベクトルの外積を求めればよい のいずれにも垂直なベクトルを求める 直線の方程式は と解釈する。 分母にがあるが、これは, 2 3 3 8 1 0 =− − − = − y x z図2 等速直線運動 時刻 t 0 =0 sで位置 x 0 =0 mから x 軸上正の向きに転がりはじめたボールが、 t 1 =10 sで x 1 =10 m、 t 2 = sで x 2 = m、 t 3 =30 sで x 3 =30 m、 t 4 =40 sで x 4 =40 m、 と一定の速度で進んでいますね。 等速直線運動では「平均の速度」も「瞬間の速度」も同$2$ 点の座標 今度は $2$ 点を通る直線の方程式を求めましょう. $2$ 点 $(x_1,y_1),(x_2,y_2)$ を通る直線の方程式を考えます.
直線,是一個點在平面或空間沿著一定方向和其相反方向運動的軌跡,是不彎曲的線。 直線是幾何學的基本概念,在不同的幾何學體系中有著不同的描述。 在這裡主要描述歐幾里得空間中的直線。 其他曲率非零狀況下的直線,請參考非歐幾里得幾何。 歐幾里得幾何研究曲率為零的空間下狀況,它標準差、標準化、相關係數和迴歸直線公式。整理起來,方便記憶。 年級 高中 所有年級, Keyword 標準差,標準化,相關係數,迴歸直線,公式(公式Ⅱの解説) 2点 (a, b), (c, d) を通る直線の方程式をいきなり考えると,点が2つもあってポイントが絞りきれないので,1点 (a, b) を優先的に考える. すなわち,2つ目の点 (c, d) は傾きを求めるための材料だけに使う. このとき,2点 (a, b), (c, d) を通る直線の傾きは
こんにちは、ウチダショウマです。 今日は、中学生でも習う 「直線の方程式」 について、数学Ⅱの図形と方程式ではどんな知識を得られるのか、スッキリ解説しようと思います。 主に、2点を通る場合の公式の証明や、平行・垂直な場合の傾きの求め方を解説していきますが、ポイントは注)分母が0のとき、は座標軸と平行な直線 =x x 1、 =y y 1となる。 ④ 2直線の位置関係 2直線の傾きが、,m m 1 2 のとき 平行: =m m 1 2 (一致の場合も平行に含めた) 垂直: 1 2 1 m m =(または、 m m 1 2 × = 1) さらに、余裕があれば以下の公式も知っていると良い2点を通る直線の方程式 切片を用いた直線の方程式 2直線の交点の座標 3点の座標で囲まれる三角形の面積 座標点で囲まれる多角形の面積 座標の回転 座標軸の回転 直交座標から極座標へ変換 極座標から直交座標へ変換
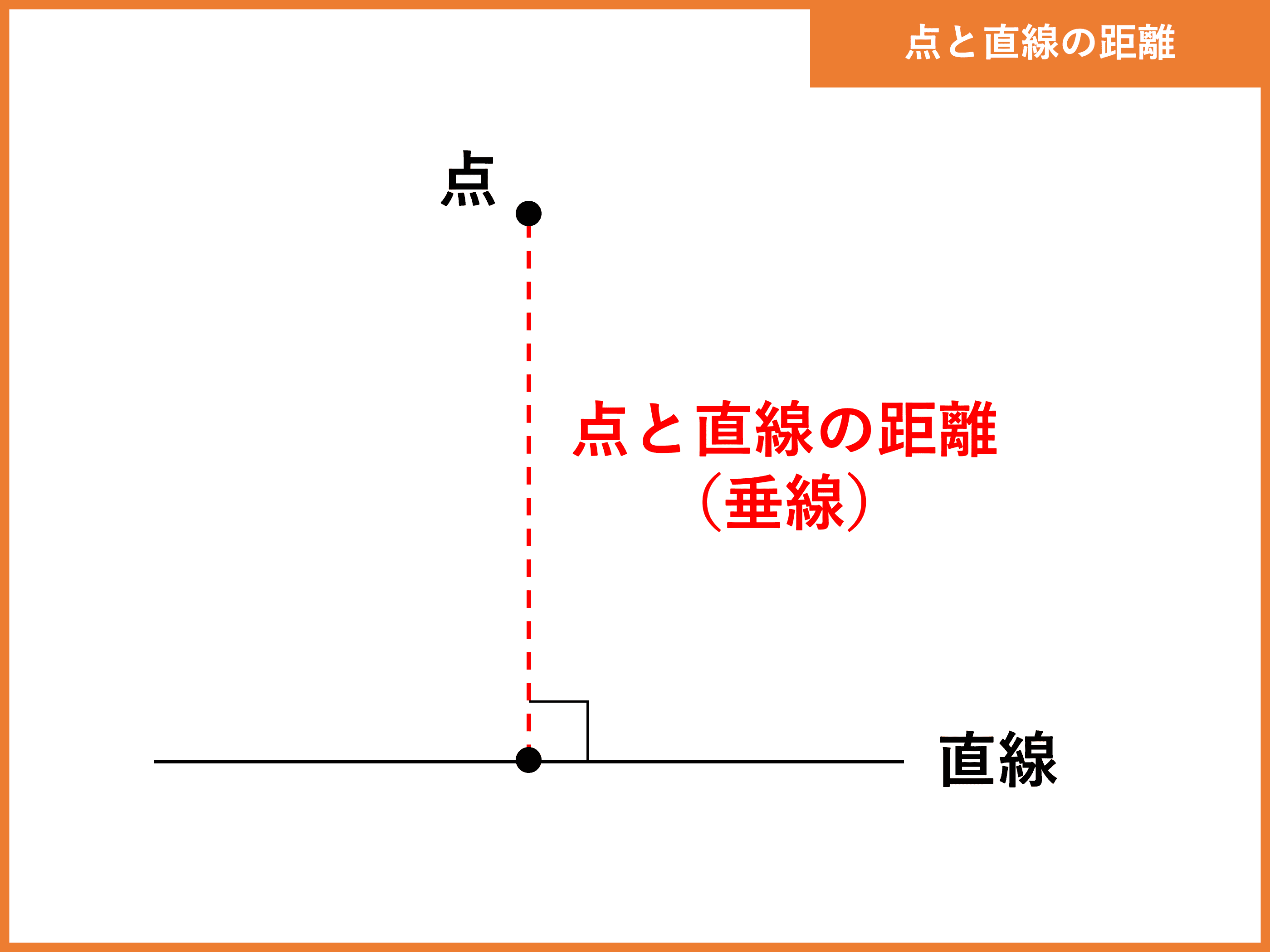


点と直線の距離とは 公式や証明 計算問題 受験辞典


放物線上の2点を通る直線 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ
放物線と直線の面積公式 2つの三角形に分けて面積を求めるなんて面倒だな そう感じているアナタ! 朗報です。 この面積を一発で求めることができる公式があります。 それがコレ!44 回帰直線を求めてみよう ←前へ|もくじ|次へ→ じゃあ、最高気温(x)と客数(y)のデータを使って、回帰直線をもとめてみます。 まず、相関係数を求めます。 そのためには、x,yの平均と標準偏差、それから偏差、偏差積をまず計算します。 そうしてから、点と直線の距離の公式はしっかりと覚えておく必要があります。覚えるときは、 ax_0by_0c は伸ばしていった法線ベクトルの先なので、元の点の座標値を代入しなければいけない。 また、法線ベクトルからどちら向きに伸びるかわからないので、絶対値をつける必要がある


高校数学 直線に対して対称な点の公式 未設定



直線と直線の距離の公式と最近点 理数アラカルト
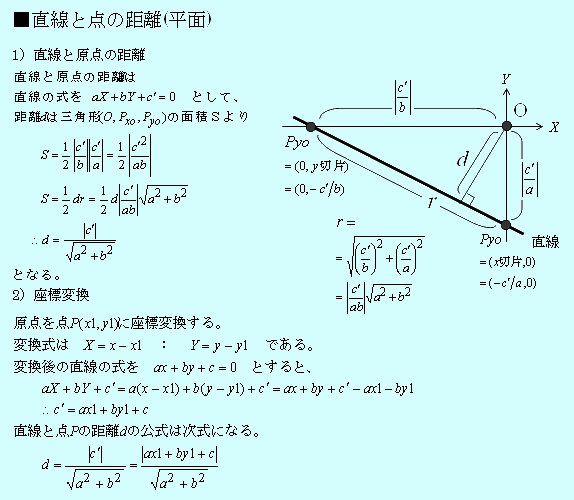
回帰直線の一般的な求め方 求め方は,点の個数は3個から n 個になったものの,2.回帰直線(具体例1)で解説した方法と同じです.すなわち,「失われた情報(lost information)を最小にする」直線の方程式を求めます. 求める直線の方程式(回帰直線)を y = a 0 a 1 x とする.このとき,回帰直線 テストの得点(Y)を勉強時間(X)で説明するにあたって、ここでは、一次関数 \(\displaystyle y=abx\) を利用する \(\displaystyle テストの得点(y)=ab\times 勉強時間(x)\) 回帰直線 この一次関数から得られる直線 切片(a) 説明変数が最小の場合のYの値問 点A(x₁, y₁)と直線 axbyc=0 の距離 d はd=ax₁by₁c/√(a²b²)である.これを示せ.<3 つの証明>阪大の13年入試問題で



図形と方程式は2時間で解けるようになる 外資系コンサルタントが主夫になったら
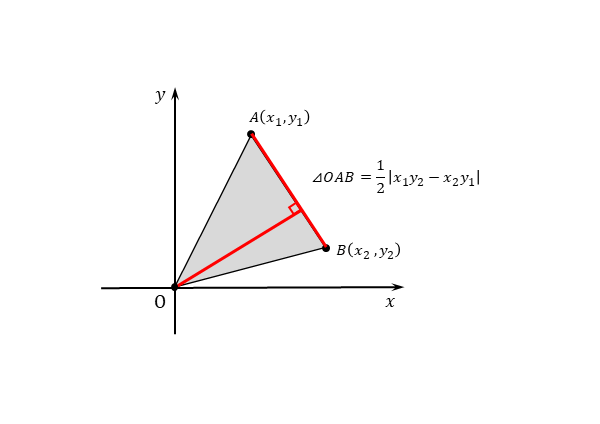


図形と方程式 三角形の面積について 日々是鍛錬 ひびこれたんれん
点(a,b)を通り傾きmの直線の方程式は y-b=m(x-a) で表わされます. この公式に当てはめたとき,次のうち対応しているものを選びなさい. (ルール:一つクリックし,続けて「対応しているもの」をクリックすると消えます.公式から分かる回帰直線の性質とは? Tooda Yuuto 16年12月24日 / 18年11月27日 回帰分析とは、 説明変数 \(x\) によって目的変数 \(y\) の変動を \(y=f(x)\) の形でどの程度説明できるのかを分析 す2直線の交点の公式をおしえてほしい。。 こんにちは!この記事をかいているKenだよ。アップルパイは1日2本だね。 よく最近、 2直線の交点の座標をもとめる公式 ってあるの?? ってきかれるんだ。 そう。 むちゃくちゃ頻繁に。。
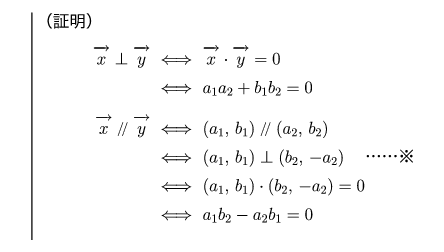


中3 2直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと



なぜ 平行な直線の方程式は 0になるのですか Clear
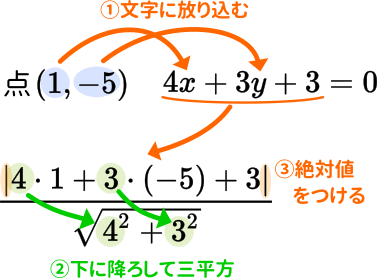
三次関数を直線で分割したときに囲まれる面積s1とs2の和を求めたい。s1=s2となるのは真ん中の点が変極点になるときだが、面積の和はどうなるのだろうか。 で 1/12公式に一致する。2点を通る直線の方程式 2つの点(x₁、y₁)と(x₂,y₂)を通る直線の方程式は、次の公式で求めます。 で直線の傾きを求めていることに注目です。 練習問題 点(3、2)と(5,4)を通る直線の方程式を求めなさい。 先ほどの公式に値をというような公式についてしっかり向き合ってみよう!というコーナーです。その初回として「点と直線の距離」をpick up してみました。ぜひ一度、考えてみてくださいね。 まずは、公式の紹介をしましょう! 数学Ⅱの「図形と方程式」で登場する公式です
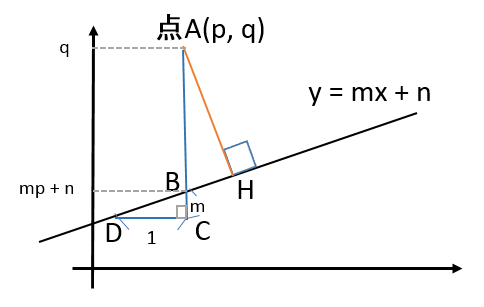


中学生でもわかる 点と直線の距離の公式の証明 偏差値40プログラマー
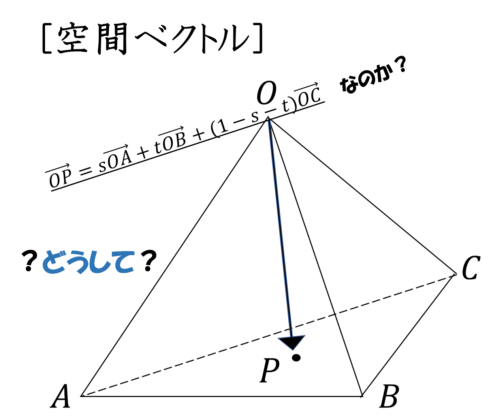


空間ベクトル S T U 1の公式の導出とその応用 Cupuasu クプアス
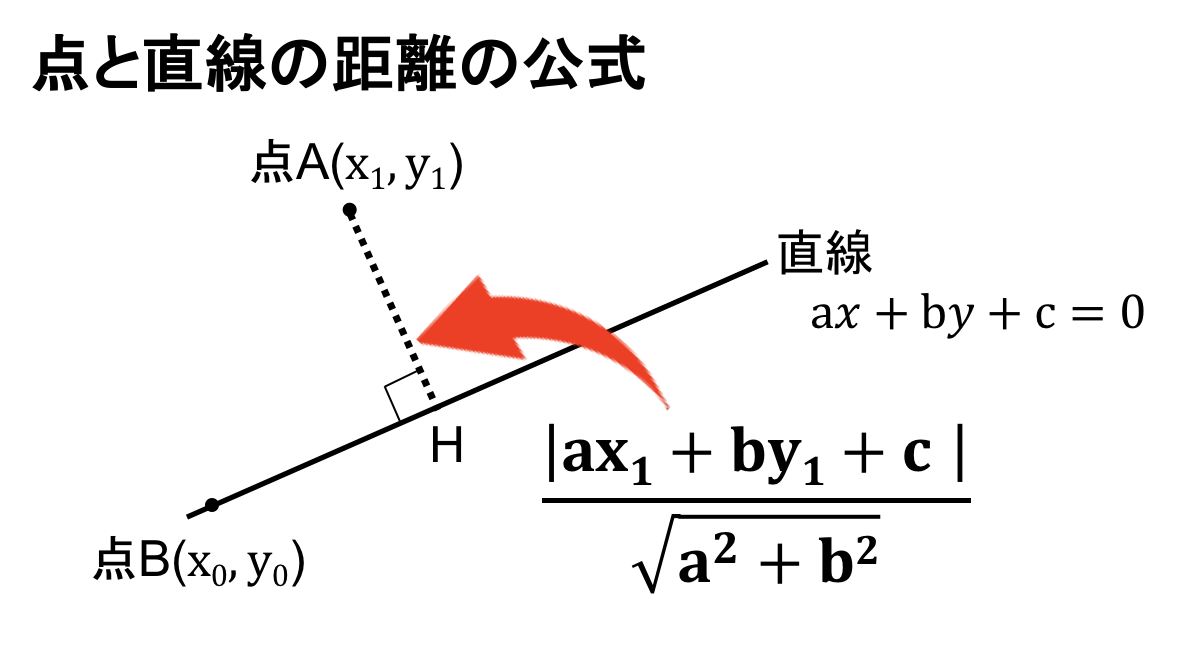
赤い直線の大きさは、余弦定理より 4×cos60° = 4× ½ = 2 です。 よって、求める内積の値は 5×2 = 10 となります。 これを一般化して考えてみましょう。 平面ベクトル→aと→bの内積は、2つのベクトルが成す角をαとおくと、 この公式が成り立つことがわかり点 (x 0, y 0) から直線 a x b y c = 0 への垂線の長さは, (言い換えると 点 (x 0, y 0) と直線 a x b y c = 0 との距離は,) a x 0 b y 0 c a 2 b 2 となる. 導出計算 点 (x 0, y 0) をP点とする.このP点から直線 a x b y c = 0 へ下ろした垂線の足を点Qとし,その点と直線の距離を求める公式を使ってみよう! 点と直線の距離を求める練習問題 点と直線の距離を求める公式まとめ! 数学の成績が落ちてきたと焦っていませんか? こちらの関連記事はいかがで


1次関数の決定 数学 二次関数 数学公式まとめ大全



直線の方程式 数学ii フリー教材開発コミュニティ Ftext



高校物理力学講座 2 等加速度直線運動をマスターしよう 前編 高校物理の攻略部屋
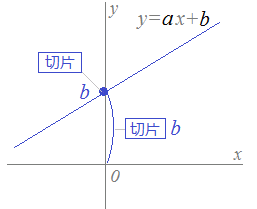


1次関数 グラフ 直線の方程式



直線と点との距離を求める公式 2013年大阪大学文系前期入試問題から 身勝手な主張
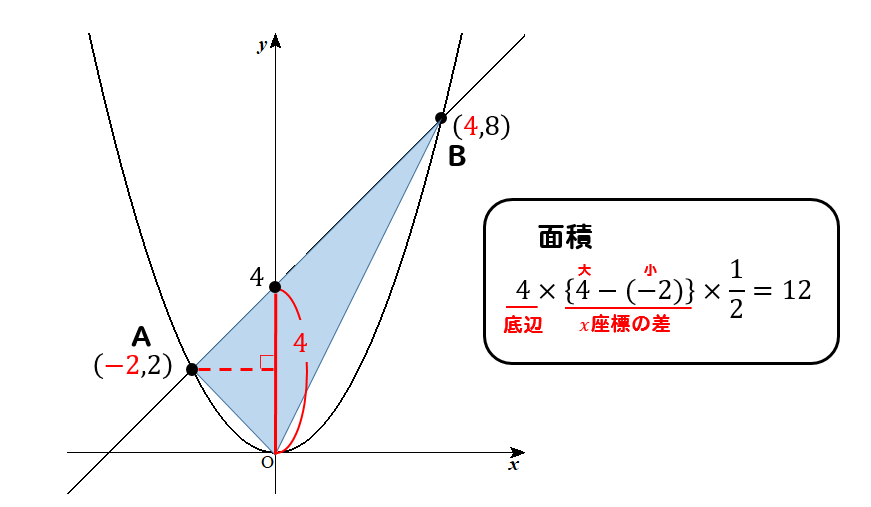


中学数学 放物線と直線の面積を求める公式は 数スタ



標準 定点を通る直線 なかけんの数学ノート


放物線上の2点を通る直線の式 から 切り取られる線分の長さ へ うしブログ


点と直線の距離
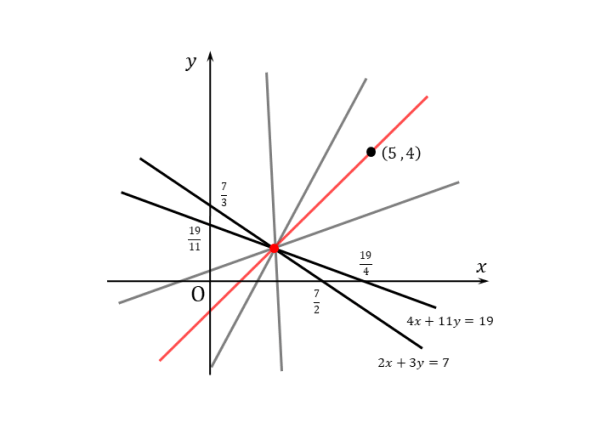


図形と方程式 2直線の交点を通る直線について 日々是鍛錬 ひびこれたんれん


直線の式の求め方 思考力を鍛える数学
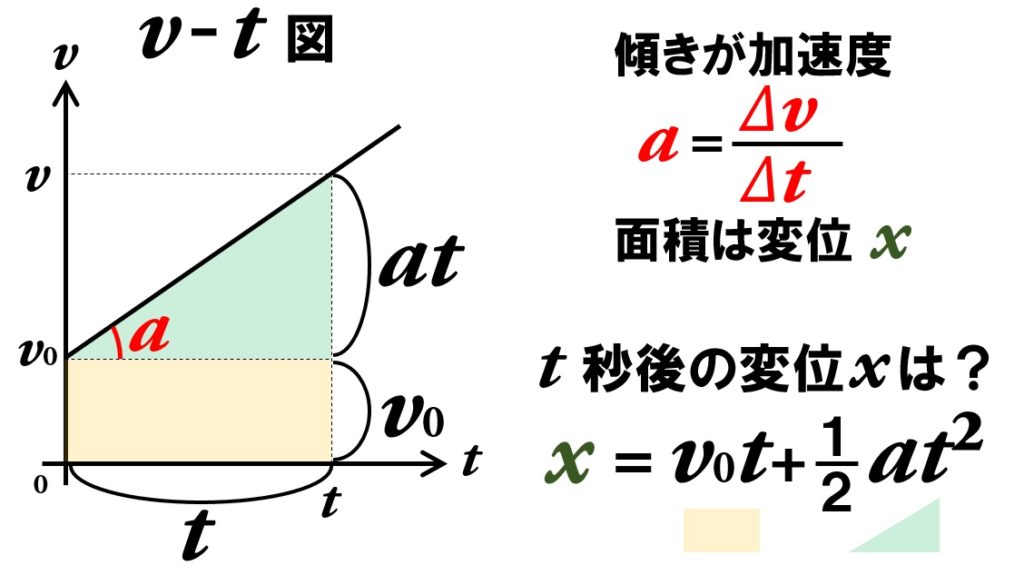


物理基礎 等加速度直線 公式の導出と練習問題 Tekibo
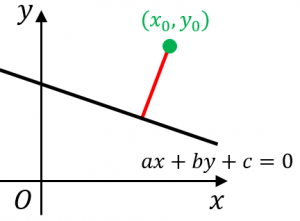


点と直線の距離の公式の意味と中学数学範囲での証明 具体例で学ぶ数学
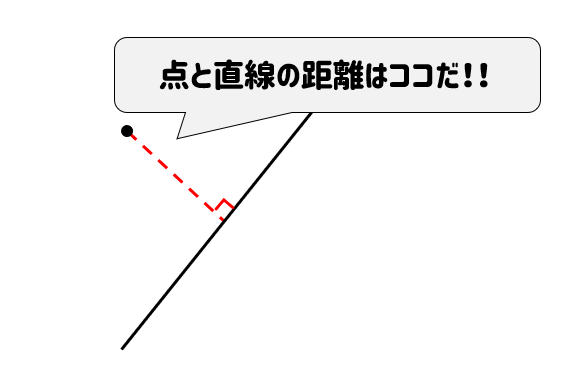


点と直線の距離 公式の覚え方と使い方をイチから解説するぞ 数スタ



円と直線の関係 判別式と点と直線の距離 高校数学の知識庫



3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ


点と直線の距離の公式 正射影ベクトルを用いた証明法 ぷっちょのput Your Hands Up


等加速度直線運動 物理学解体新書


直線と点との距離 高精度計算サイト



等加速度直線運動の3公式 高校物理をやさしく解説するブログ



点と直線の距離公式をベクトルを使って導く すうがくブログ 式変形ch


数 図形と方程式 点と直線の距離の公式をビジュアルで覚える Mm参考書



ベクトル方程式を超わかりやすく解説した 理系ラボ



積分の面積公式と証明 6分の1公式 接線など 理系ラボ


点と直線の距離 佐々木数学塾
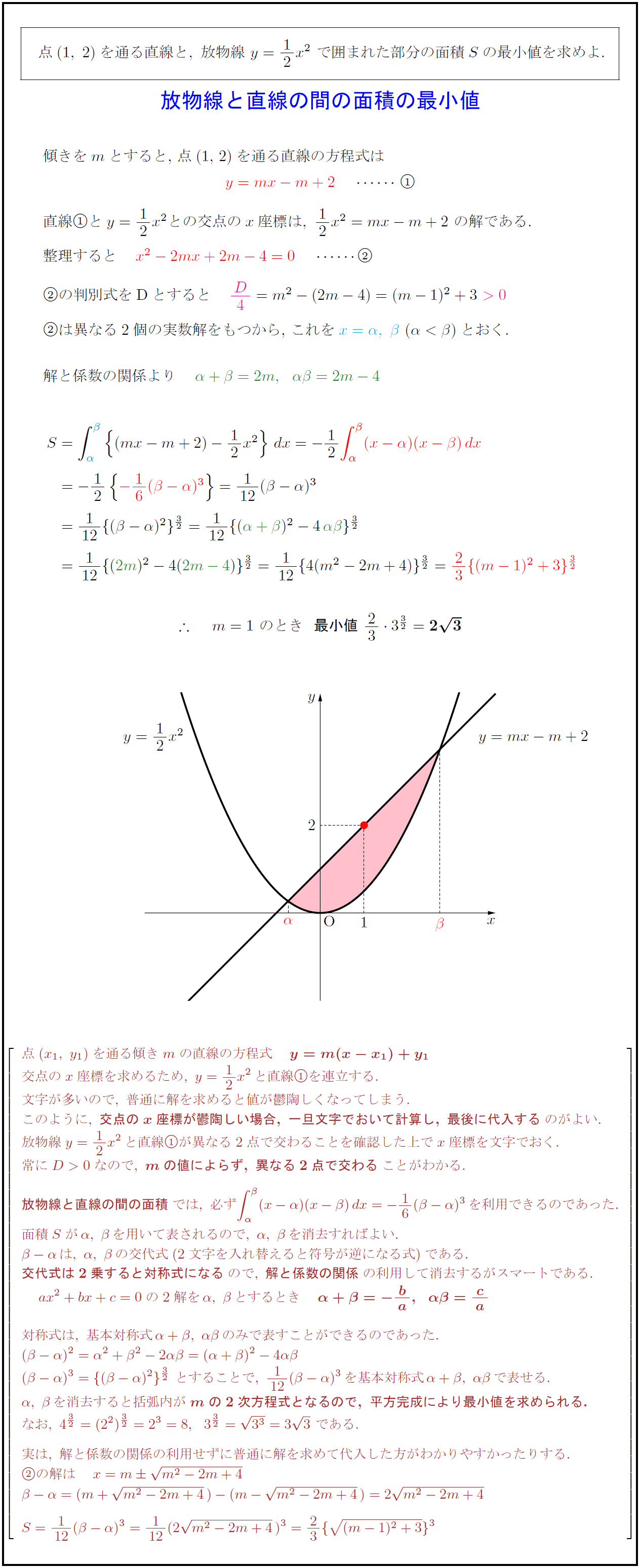


高校数学 放物線と直線の間の面積の最小値 1 6公式の利用 受験の月
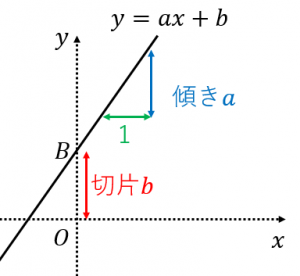


傾きと切片の意味と求め方を丁寧に解説 具体例で学ぶ数学



1次関数 直線の傾きを求める計算 中学数学 定期テスト対策サイト



等速直線運動のグラフ 公式もわかりやすく解説 Dr あゆみの物理教室



等加速度直線運動 5つの物理量を暗記して 公式を使いこなそう 平川ブログ



必読 加速度 等加速度直線運動の3公式まとめ 物理のいろは



等加速度直線運動の3公式の使い方がわかりません 理科 苦手解決q A 進研ゼミ高校講座



単回帰分析 最小二乗法の公式はどうすれば求められるのか 統計上の誤差と残差の違い アタリマエ


2点 直線の方程式


切片とは 1分でわかる意味 求め方と公式 読み方 傾きとの違い



高校数学 直線の方程式 基本形 一般形 切片形 受験の月



数学 高校の教科書を見ています 数学 教科書 除算



直線の方程式 数学ii フリー教材開発コミュニティ Ftext


中3数学 2次関数総合 頂点を通らない三角形の2等分線



関数07 放物線と直線の公式 Youtube



簡単公式 2直線の交点の座標を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



点と直線の距離の公式とその使い方 高校数学の知識庫



数学 図形と方程式 点と直線の距離 の公式の導出 オンライン無料塾 ターンナップ



物理 等加速度直線運動の3公式は絶対覚える 岡山医学科進学塾のブログ



図形と方程式 直線の方程式について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



点と直線の距離の公式とは 3次元やベクトルを用いた証明も解説 阪大入試問題 遊ぶ数学塾



微分を使った接線に垂直な法線の方程式の求め方と公式


数学用語解説 数 図形と方程式 軌跡と領域


2点間の距離とは 1分でわかる意味 公式と計算方法 座標との関係



一次関数 直線の式がわかる4つの求め方 Qikeru 学びを楽しくわかりやすく


点と直線の距離の公式


原点と直線の距離の公式の証明 図形と計量



点と直線の距離 交点をmatplotlibで作図する もものきとデータ解析をはじめよう



点と直線の距離 画像処理ソリューション



点と直線の距離公式の3通りの証明 高校数学の美しい物語



三角形の成立条件と面積の求め方を解説 図形と方程式



2次方程式の解の公式の一般化 高校数学に関する質問 勉強質問サイト


放物線上の2点を通る直線の式 から 切り取られる線分の長さ へ うしブログ
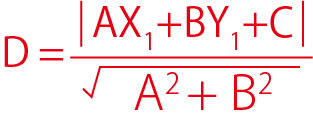


点と直線の距離の公式の覚え方 証明の方法や練習問題も解説 高校生向け受験応援メディア 受験のミカタ
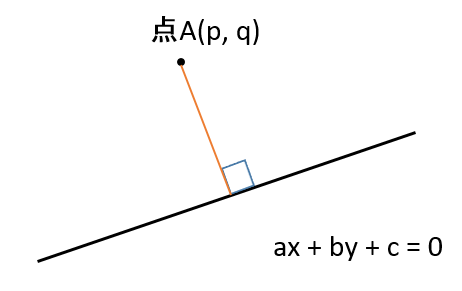


中学生でもわかる 点と直線の距離の公式の証明 偏差値40プログラマー



直線の方程式 2点を通る の公式を証明 平行や垂直な場合の傾きの求め方も解説 遊ぶ数学塾



点と直線の距離の公式の覚え方 証明の方法や練習問題も解説 高校生向け受験応援メディア 受験のミカタ



難関高校合格のための中学数学公式一覧 10秒で解けますか


円と直線の位置関係 思考力を鍛える数学



高校数学 直線の傾きによる2点間の距離の公式 放物線の弦の長さ 受験の月
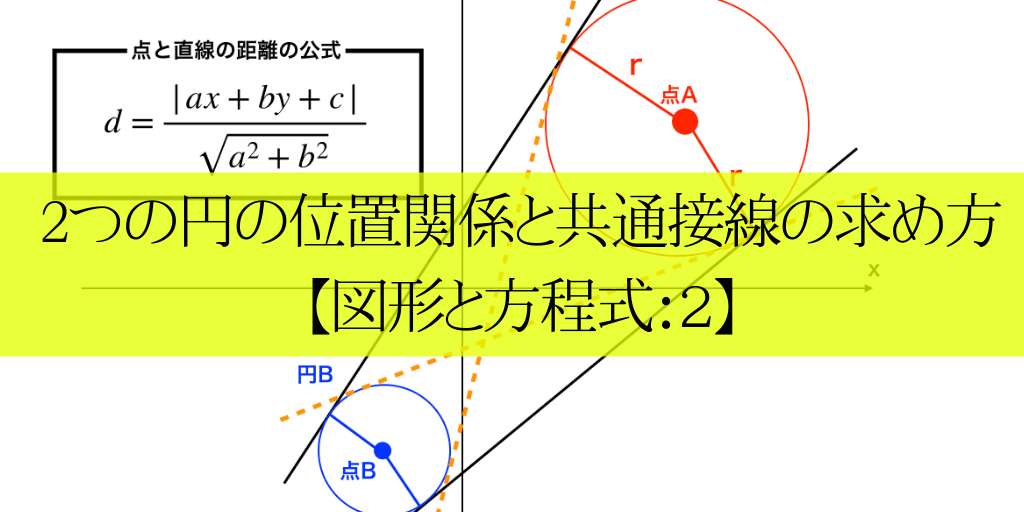


2つの円の位置関係と共通接線の求め方 図形と方程式 2


直線と放物線の面積算出の1 6公式 Thoth Children



高校数学 直線の方程式 練習編 映像授業のtry It トライイット



回帰直線 2



点と直線の距離を求める公式とその証明 数学ii By ふぇるまー マナペディア



座標上の2つの直線が垂直に交わるための条件 公式 数学ii By ふぇるまー マナペディア
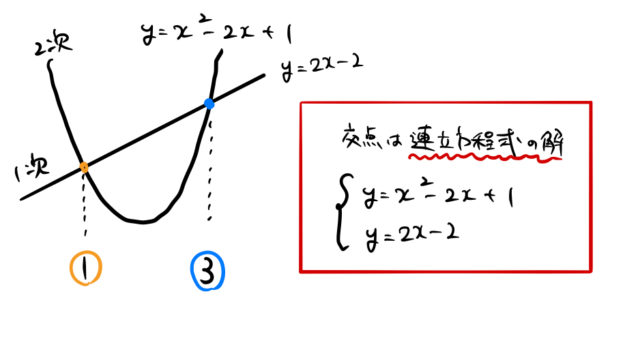


高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら



高校数学 点と直線の距離の公式 映像授業のtry It トライイット
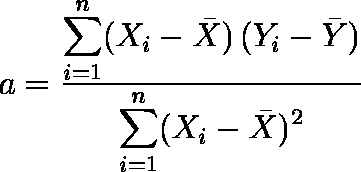


直線回帰とは何 Weblio辞書



直線の方程式 数学ii フリー教材開発コミュニティ Ftext



数学公式 点と直線の距離の公式 は2次試験の前に 証明を確認しておきたい 学習村の とりあえず国公立へ行こう
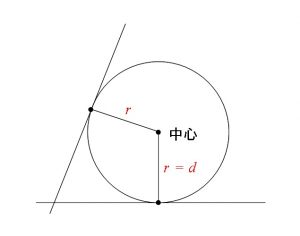


円に接する直線 接線の方程式 の求め方3パターン
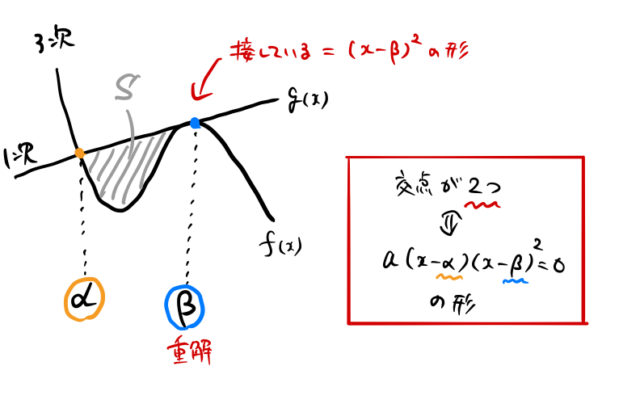


高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら


2直線の交点を通る直線の方程式がなぜこのような式になるのかわか Yahoo 知恵袋



3つの証明 点と直線の距離の公式 D Ax By C A B 数学ii Youtube



中3 2直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと


直線の式の求め方 思考力を鍛える数学



円と直線 高校数学に関する質問 勉強質問サイト



直線の方程式ax By C 0型の意味と垂直条件 平行条件 ラディカル高校数学



直線の公式 Youtube
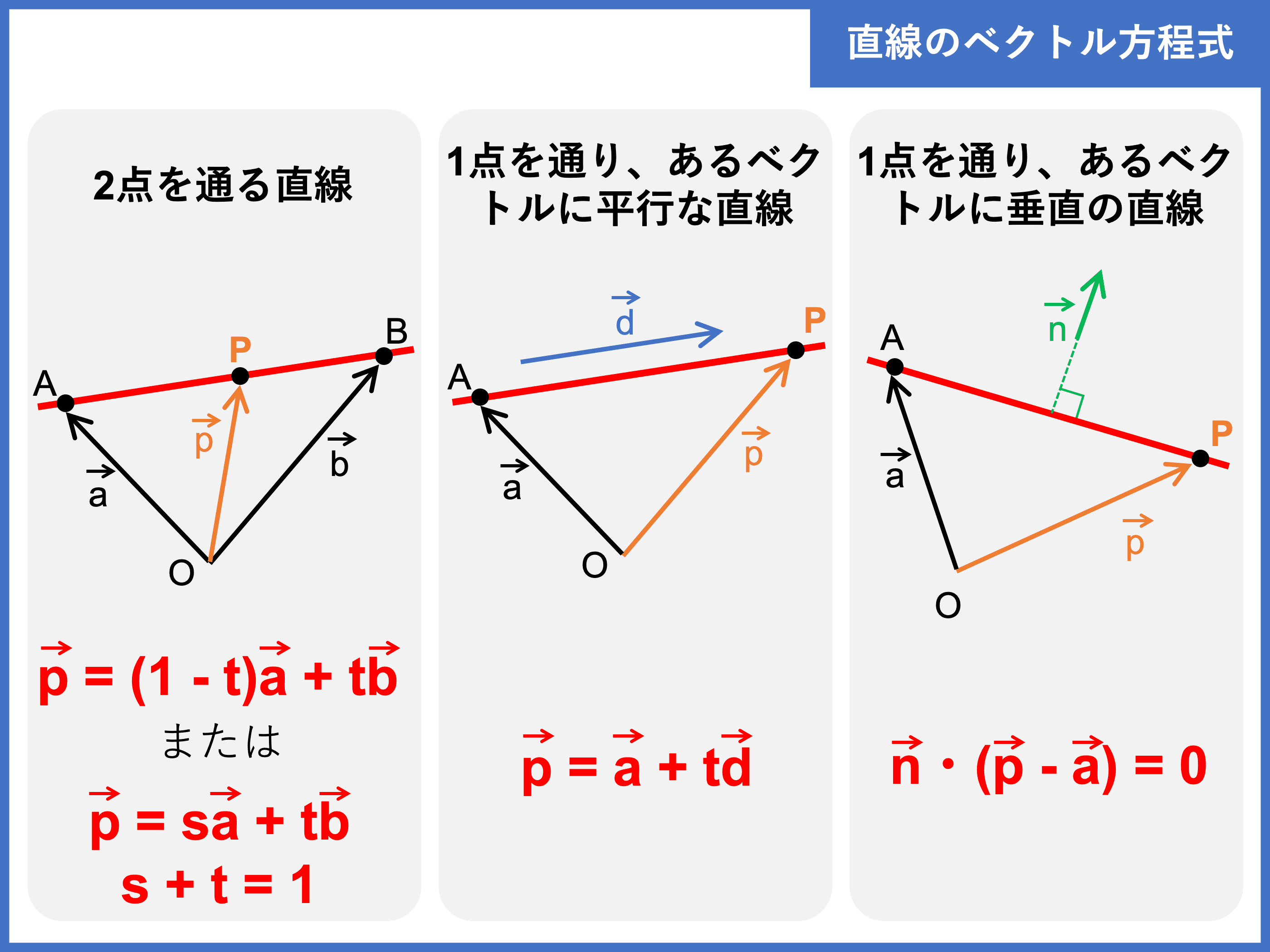


ベクトル方程式とは 図形別の公式 直線 円 や問題の解き方 受験辞典



点と直線の距離の公式で分子の絶対値を外したら にならないんですか Clear
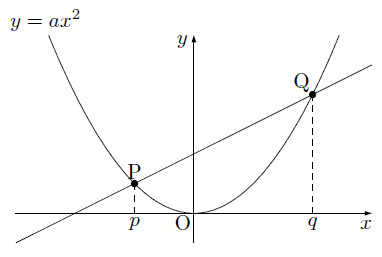


放物線と直線の式 まなびの学園



点と直線の距離とその証明 おいしい数学



直線と直線の距離の公式と最近点 理数アラカルト



0 件のコメント:
コメントを投稿